Como calcular porcentagem? Passo a passo para não errar!

Você já parou para pensar em quantas vezes por dia se depara com o símbolo de porcentagem (%)? Seja na etiqueta de uma promoção na sua loja favorita, uma questão na prova do vestibular ou Enem, nos juros do cartão de crédito, nos noticiários sobre economia ou até mesmo na bateria do seu celular, o cálculo de porcentagem está em toda parte.

Aprender como calcular porcentagem é mais simples do que parece e é uma habilidade fundamental não só para ir bem nas provas, mas para tomar decisões mais inteligentes no dia a dia. Neste guia completo, explicar como calcular porcentagem, desde o conceito básico até as aplicações práticas e os macetes para resolver questões de vestibular. Confira!

O que é porcentagem?

A palavra “porcentagem” vem do latim per centum, que significa “por cem”. De forma simples, a porcentagem é uma maneira de expressar uma proporção ou uma fração de um todo, dividindo esse todo em 100 partes iguais.

Pense em uma pizza cortada em 100 pedaços. Se você comer 25 pedaços, você comeu 25% da pizza. Se comer 50 pedaços, comeu 50%, ou seja, metade.

A grande vantagem da porcentagem é que ela nos dá uma base de comparação universal. Dizer “acertei 20 questões” não informa muito, mas dizer “acertei 80% da prova” deixa claro o seu excelente desempenho, independentemente do número total de questões. Por isso, ela é essencial para a educação matemática, finanças pessoais e a interpretação de dados.

Como calcular porcentagem: métodos básicos

Existem diferentes caminhos para chegar ao mesmo resultado quando o assunto é cálculo de porcentagem. A escolha do método ideal depende da situação, das ferramentas que você tem em mãos e, claro, da sua preferência pessoal. Veja um passo a passo de como calcular porcentagem com os três métodos mais comuns:

Fórmula básica para calcular porcentagem

Este é o método mais direto e fundamental. Existem duas situações principais onde você vai usar uma fórmula.

1. Para descobrir o percentual que um valor (parte) representa de outro (todo):

A fórmula é: (Parte / Todo) * 100

• Exemplo prático: Em uma sala com 40 alunos, 10 usam óculos. Qual é o percentual de alunos que usam óculos?
  • Parte: 10 (alunos de óculos)
  • Todo: 40 (total de alunos)
  • Cálculo: (10 / 40) * 100 = 0,25 * 100 = 25%
  • Resposta: 25% dos alunos usam óculos.

2. Para encontrar o valor correspondente a um percentual:

A fórmula é: (Percentual / 100) * Todo

• Exemplo prático: Você quer comprar um livro que custa R$ 80 e conseguiu um cupom de 15% de desconto. Qual o valor do desconto em reais?
  • Percentual: 15
  • Todo: 80 (preço do livro)
  • Cálculo: (15 / 100) * 80 = 0,15 * 80 = R$ 12
  • Resposta: O desconto é de R$ 12.

Uso de calculadora para porcentagens

Na correria do dia a dia, a calculadora (seja a do celular ou uma calculadora online) é sua melhor amiga. A maioria delas tem uma tecla específica para porcentagem (%) que simplifica o processo.

• Para calcular um percentual de um valor: Digite o valor total, o sinal de multiplicação (x), o percentual e, por fim, a tecla % e aperte o botão de igual (=).
  • Exemplo: Para achar 25% de 200, você digita: 200 x 25 % e o =. O resultado (50) aparecerá instantaneamente na tela.
• Para calcular aumento ou diminuição percentual:
  • Aumento: Para aumentar 15% em um valor de R$ 300, digite: 300 + 15 %, aperte o botão de igual (=). O resultado será R$ 345.
  • Diminuição: Para um desconto de 20% em um valor de R$ 500, digite: 500 - 20 %, aperte o botão de igual (=). O resultado será R$ 400.

Método da regra de três simples

A regra de três se encaixa perfeitamente no cálculo de porcentagem. O princípio é simples: você relaciona duas grandezas, sabendo que o valor total corresponde sempre a 100%.

• Exemplo prático: Um produto que custava R$ 250 teve um aumento e agora custa R$ 280. Qual foi o aumento percentual?
  1. Organize as grandezas: O valor original (R$ 250) é o nosso 100%. O aumento foi de R$ 30 (280 – 250). Queremos saber qual percentual esses R$ 30 representam.
  2. Monte a regra de três:
     • R$ 250 —— 100%
     • R$ 30 —— X %
  3. Multiplique em cruz:
     • 250 * X = 30 * 100
     • 250X = 3000
  4. Resolva a equação:
     • X = 3000 / 250
     • X = 12
  • Resposta: O aumento foi de 12%.

Aplicações práticas de porcentagem no dia a dia

Entender a teoria é importante, mas ver como a porcentagem funciona na prática é o que realmente faz a diferença.

Exemplos de como a porcentagem é usada em finanças pessoais

Gerenciar seu dinheiro fica muito mais fácil quando você domina o cálculo de porcentagem.

• Orçamento: Se sua renda mensal é de R$ 4.000 e você gasta R$ 1.200 com moradia, pode calcular que 30% da sua renda ((1200 / 4000) * 100) é destinada a essa despesa. Isso ajuda a visualizar para onde seu dinheiro está indo.
• Investimentos: Se você investe R$ 5.000 e obtém um rendimento de 8% ao ano, sabe que seu lucro será de R$ 400 ((8 / 100) * 5000).
• Juros: Entender os juros do cartão de crédito, que são expressos em porcentagem, é vital para evitar dívidas. Uma taxa de 14% ao mês sobre um saldo devedor de R$ 1.000 significa um acréscimo de R$ 140 só de juros naquele mês.

Importância da porcentagem em descontos e promoções

Quem não gosta de uma boa promoção? Saber calcular o desconto real ajuda a avaliar se a oferta vale mesmo a pena.

Imagine uma TV de R$ 3.000 com 20% de desconto. O cálculo rápido mostra que o desconto é de R$ 600, e o preço final será R$ 2.400. Essa habilidade permite comparar ofertas entre lojas e identificar as melhores oportunidades, garantindo que você está fazendo um bom negócio.

Uso de porcentagem em estatísticas e dados

Jornais, portais de notícias e pesquisas científicas usam porcentagens o tempo todo para apresentar dados de forma clara e concisa.

• Pesquisas de Opinião: “65% dos entrevistados aprovam a nova lei.”
• Dados Econômicos: “A inflação do mês foi de 0,5%.”
• Saúde: “A eficácia da vacina é de 95%.”

Saber o que esses números significam permite que você interprete as informações criticamente, em vez de apenas aceitá-las.

Principais fórmulas e conceitos de porcentagem

Para consolidar seu aprendizado, vamos revisar os conceitos e fórmulas mais importantes que você precisa ter na ponta da língua:

• Aumento Percentual: Para calcular um valor final após um aumento, use a fórmula: Valor Final = Valor Inicial * (1 + (Taxa Percentual / 100)). Por exemplo, um aumento de 10% sobre R$ 100 é 100 * (1 + 0,10) = 100 * 1,10 = R$ 110.
• Diminuição Percentual: Para calcular um valor final após um desconto, a fórmula é: Valor Final = Valor Inicial * (1 - (Taxa Percentual / 100)). Um desconto de 20% sobre R$ 100 é 100 * (1 - 0,20) = 100 * 0,80 = R$ 80.
• Variação Percentual: Para descobrir a variação entre dois valores, use: ((Valor Novo - Valor Antigo) / Valor Antigo) * 100.

Como a porcentagem é abordada no Enem e vestibulares

Se você está se preparando para o Enem ou outros vestibulares, saiba que a porcentagem é um dos tópicos mais recorrentes na prova de Matemática e suas Tecnologias. Dificilmente você fará uma prova sem encontrar pelo menos uma questão que envolva esse conceito.

As questões costumam ser contextualizadas, exigindo interpretação de texto e raciocínio lógico, e não apenas a aplicação de uma fórmula. Geralmente, a porcentagem aparece combinada com outros assuntos, como juros simples e compostos, probabilidade, análise de gráficos e tabelas.

Exemplo 1

(Enem 2024)

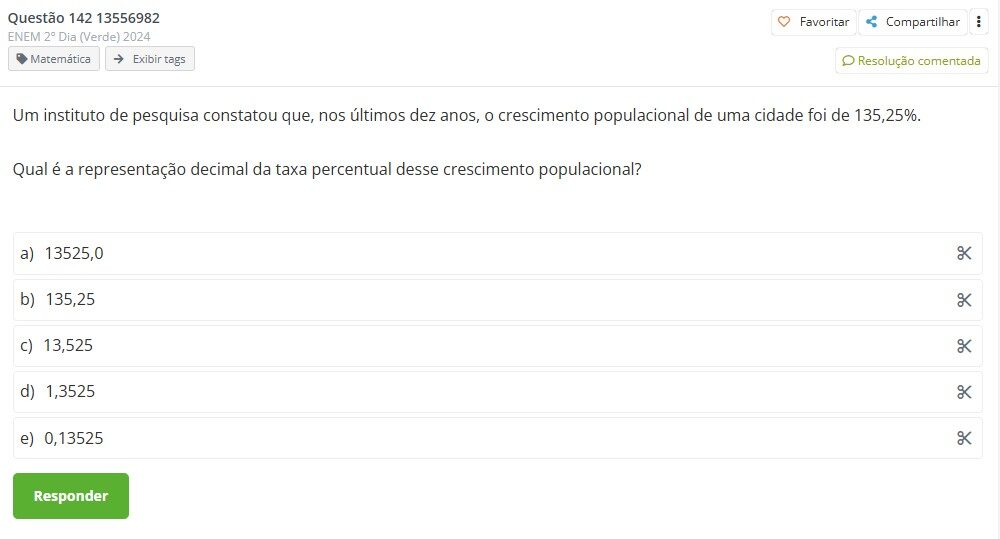
Resolução:

Para entender a conversão de uma taxa percentual em sua representação decimal, é importante lembrar que a taxa percentual é uma maneira de expressar uma proporção em relação a 100.

Quando dizemos que o crescimento populacional foi de 135,25%, isso significa que, para cada 100 unidades da população original, houve um aumento de 135,25 unidades. Para converter essa porcentagem em um número decimal, seguimos um procedimento simples:

1. Conversão de percentual para decimal: Para fazer essa conversão, dividimos a taxa percentual por 100. Portanto, a taxa percentual de 135,25% pode ser convertida para decimal da seguinte maneira:

2. Realizando a divisão: Agora, vamos calcular:

Assim, a representação decimal de 135,25% é 1,3525. Portanto, a resposta correta é 1,3525, que é a forma decimal da taxa de crescimento populacional.

Exemplo 2

(Enem 2021)

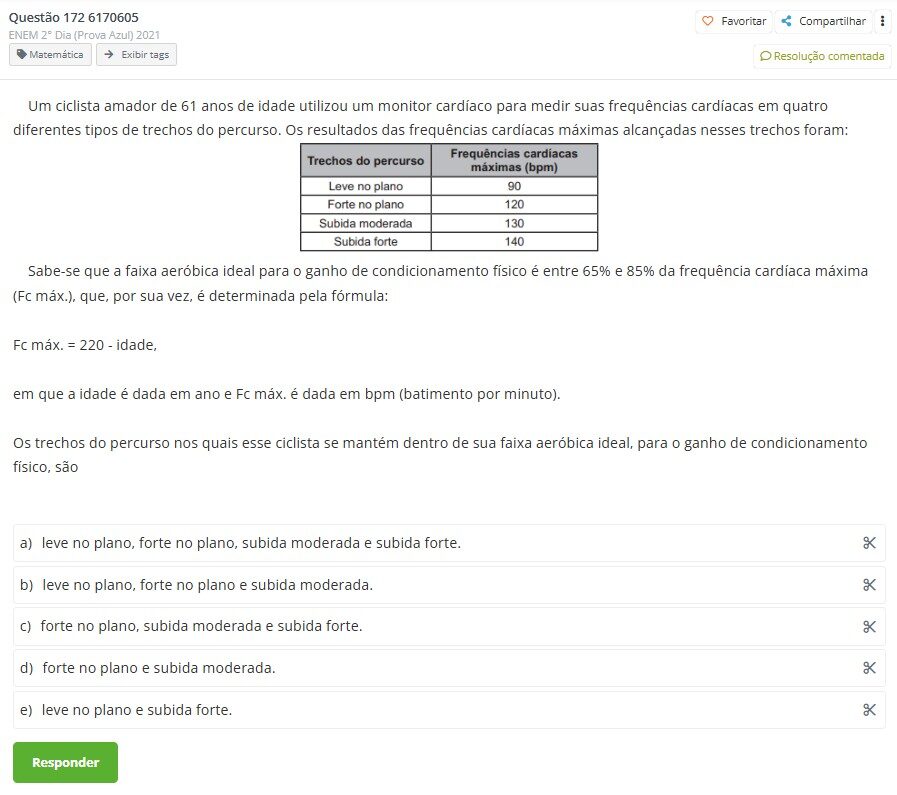
Resolução:

Para achar o intervalo de frequência razoável, temos:

E, sendo o ideal um intervalo entre 65-85% da , então:

Assim, os trajetos ideais seriam os de intensidade forte no plano e de subida moderada.

Logo, alternativa correta letra D.

Acesse essas e mais questões de porcentagem do Enem e vestibulares na Plataforma Estuda.com

Resumo de como calcular porcentagem

Dominar o cálculo de porcentagem é uma habilidade que abre portas para o Enem e vestibulares, bem como na sua vida acadêmica, profissional ou pessoal. Vamos recapitular os postos-chave para você nunca mais esquecer:

• O que é? Porcentagem é uma fração com denominador 100, usada para representar partes de um todo.
• Como calcular? Você pode usar a fórmula básica (Parte / Todo) * 100, a prática regra de três simples ou a tecla de porcentagem (%) da sua calculadora.
• Aumento e Desconto: Lembre-se dos fatores de multiplicação. Para um aumento de 15%, multiplique por 1,15. Para um desconto de 25%, multiplique por 0,75.
• Onde se aplica? Em tudo! Finanças, compras, estatísticas, notícias, provas e muito mais.

Sendo assim, a melhor maneira de se sentir confiante é praticar. Comece a calcular os descontos nas lojas, pratique com questões e busque interpretar os dados que você vê por aí. Logo, o cálculo de porcentagem se tornará uma tarefa automática e intuitiva para você.