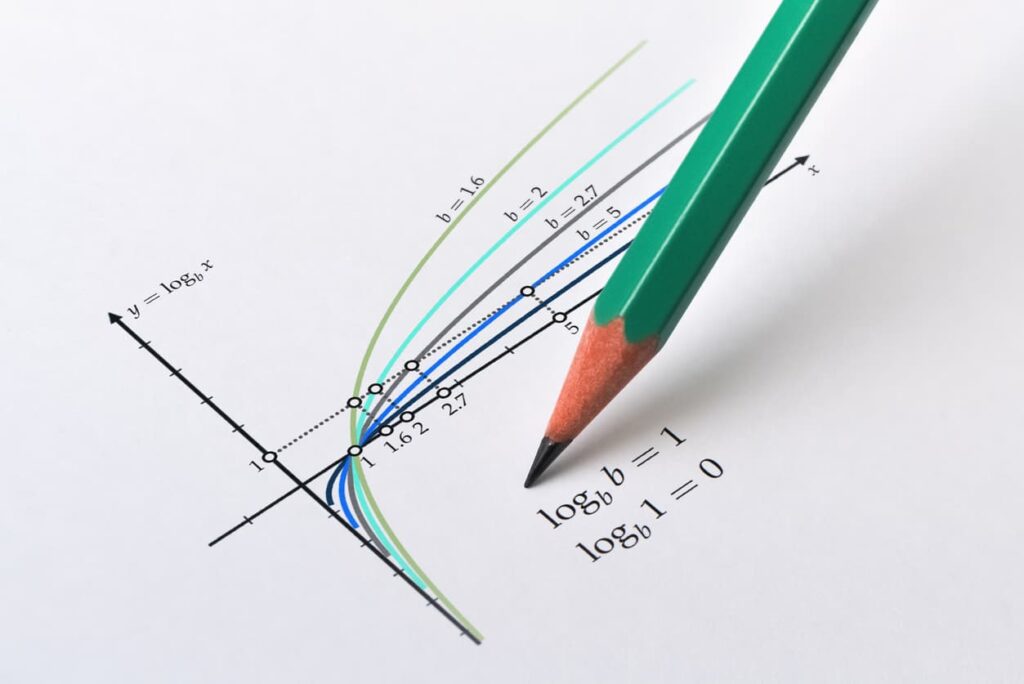
A matéria de logaritmo pode ser uma trava para diversos estudantes, principalmente quando falamos de Matemática no Enem e vestibulares. Por isso, criamos esse conteúdo para ajudar você a ver como os logaritmos são super úteis e até legais de entender. Sério! 😉
Confira a definição de logaritmo, suas propriedades, como calcular, onde são usados e até exercícios para ver na prática! Vamos lá! 👇
Conteúdo
O que é logaritmo? Definição
Sabe quando a gente aprende que multiplicação é tipo uma “soma acelerada” e divisão é a “operação inversa da multiplicação”? Então, o logaritmo funciona de um jeito parecido com a potenciação!
Pensa assim:
- Se eu te perguntar: “Quanto é 2³?” 🤔 Você pensa: 2×2×2=8. Fácil!
- Mas e se eu te perguntar: “Qual número eu coloco no expoente do 2 pra ele virar 8?” 🤔 Tipo, 2^x=8?
É aí que entra o logaritmo! Ele é a resposta para essa segunda pergunta. No caso, a resposta é 3. Então, fica assim:
Resumindo: o logaritmo te diz qual é o expoente que você precisa colocar na base para chegar em um determinado resultado.
Condição de existência
Para um logaritmo “existir” de verdade no mundo dos números reais, ele precisa seguir umas regrinhas:
- A base (b) tem que ser maior que zero (b>0). Não faz sentido elevar um número negativo a um expoente para obter um número positivo.
- A base (b) não pode ser 1 (b≠1). Porque 1 elevado a qualquer coisa é sempre 1, então não teríamos um expoente único.
- O logaritmando (a) tem que ser maior que zero (a>0). Não tem como uma base positiva (que é a condição 1) elevada a um expoente dar um número negativo ou zero.
Propriedades dos logaritmos
As propriedades dos logaritmos facilitam muito os cálculos e simplificações de expressões logarítmicas. Veja cada uma delas com explicações e exemplos:

Logaritmo do produto
Essa propriedade afirma que o logaritmo de um produto é igual à soma dos logaritmos de seus fatores.
Logaritmo do quociente
O logaritmo de uma divisão equivale à diferença entre os logaritmos do numerador e do denominador.
Logaritmo de potência
Quando o argumento for uma potência, podemos “trazer” o expoente para frente como multiplicador.
Logaritmo da Raiz
A raiz pode ser reescrita como uma potência com expoente fracionário.
Logaritmo de 1
Isso acontece porque qualquer número elevado a zero é igual a 1: b^0 = 1
Logaritmo da base
O logaritmo de uma base nela mesma é igual a 1, pois b^1 = b
Mudança de base
Essa propriedade permite mudar a base de um logaritmo. É muito útil quando se quer calcular um logaritmo com base diferente da calculadora, que normalmente usa as bases 10 ou ‘e’.
Como calcular um logaritmo?
Para calcular um logaritmo, é preciso entender a definição básica:
Ou seja, o logaritmo responde à pergunta: “Qual o expoente que devo aplicar na base para obter o número?”
Casos exatos (valores conhecidos):
Alguns logaritmos têm resultados exatos e são importantes de memorizar:
Caso o valor não seja exato:
Você pode usar a mudança de base para transformar em uma base que a calculadora aceite:
Ou recorrer a aproximações com logaritmos decimais (base 10) ou logaritmos naturais (base ‘e’).
Onde os logaritmos aparecem no mundo real?
Logaritmos não são só pra prova de matemática, eles estão por toda parte! Olha só:
- Terremotos e a Escala Richter 🌍: cada ponto na escala Richter significa um terremoto 10 vezes mais forte! É uma escala logarítmica que nos ajuda a medir a energia liberada.
- pH de Produtos (Limpeza, Cabelo) 🧴: o pH mede a acidez ou alcalinidade. É uma escala logarítmica da concentração de íons de hidrogênio. Um pH 7 é neutro, pH 6 é 10x mais ácido que 7!
- Decibéis (Volume do Som) 🎶: a intensidade do som que a gente ouve é medida em decibéis, e a percepção do nosso ouvido é logarítmica. Um som de 70 dB não é o dobro de um de 35 dB, ele é MUITO mais intenso!
- Juros Compostos e Finanças 🤑: quer saber em quanto tempo seu dinheiro vai dobrar em um investimento? Os logaritmos ajudam a calcular isso em cenários de juros contínuos.
- Crescimento e Decaimento (População, Radioatividade) 📈📉: modelos de crescimento de populações (bactérias, pessoas) ou decaimento radioativo (usado em datação de fósseis) são descritos por funções exponenciais, e os logaritmos são a chave para desvendar essas equações.
- No seu PC/Celular (Análise de Algoritmos) 🖥️: na programação, muitos algoritmos (tipo como um programa de computador busca um item em uma lista enorme) têm sua eficiência medida logaritmicamente. Quanto maior a lista, mais rápido (relativamente) o algoritmo encontra o item!
Logaritmo exercícios
Para fixar o conteúdo aprendido, é essencial resolver exercícios. Abaixo, você confere exemplos com resoluções para o cálculo de logaritmos.
Questão FUVEST (USP) 2023
Resposta: C
Confira a resolução completa na Estuda.com e diversas questões de logaritmo e matemática!
Questão ENEM 2020 – 2° Dia (Prova Rosa)
Dúvidas frequentes sobre logaritmos (FAQ)
Qual a diferença entre “log” e “ln”?
R: “log” geralmente se refere ao logaritmo na base 10 (decimal), enquanto “ln” se refere ao logaritmo na base e (natural/neperiano).
Posso ter logaritmo de um número negativo?
R: Não, o logaritmando sempre tem que ser um número positivo (a>0).
Logaritmo pode ser zero?
R: Sim! logb 1=0, para qualquer base b>0 e b≠1.
O que é antilogaritmo?
R: O antilogaritmo é a operação inversa do logaritmo. Se logb a=x, então o antilogaritmo de x na base b é a. Ou seja, é calcular b^x.