MDC (Máximo divisor comum): o que é e como calcular

O MDC, ou Máximo Divisor Comum, aparece nos problemas de matemática que pedem para dividir objetos em grupos iguais do maior tamanho possível, por exemplo, ou na hora de simplificar uma fração ao máximo.

Nesse momento, entender o que é o MDC e como calculá-lo pode auxiliar você em diversos momentos de estudos e provas. É a matemática básica essencial para estudantes, vestibulandos e concurseiros. Neste guia completo, vamos explicar tudo sobre o Máximo Divisor Comum, desde sua definição até suas aplicações práticas. Vamos lá!

O que é o MDC?

O MDC (Máximo Divisor Comum) entre dois ou mais números inteiros é o maior número que consegue dividir todos eles sem deixar resto. Parece complicado? Vamos quebrar o conceito:

• Divisor: um número é divisor de outro quando a divisão entre eles é exata, ou seja, o resto é zero. Por exemplo, os divisores de 12 são 1, 2, 3, 4, 6 e 12.
• Divisor Comum: é um número que é divisor de dois ou mais números ao mesmo tempo. Por exemplo, os divisores de 12 e 18 são 1, 2, 3 e 6.
• Máximo Divisor Comum: é o maior de todos os divisores comuns. No exemplo de 12 e 18, o MDC é 6.

A importância do MDC vai além da sala de aula. Ele é fundamental para a resolução de problemas matemáticos, simplificação de frações e até mesmo em áreas mais avançadas como a teoria dos números e a criptografia.

Como calcular o MDC?

Existem diferentes maneiras de encontrar o Máximo Divisor Comum. Para isso, conhecer mais de um método pode te ajudar a escolher o mais eficiente para cada tipo de problema. Veja os três principais:

Método da decomposição em fatores primos

Esse é um dos métodos mais populares, especialmente para números grandes. O processo é simples:

1. Decomponha os números: fatore cada um dos números em seus fatores primos.
2. Identifique os fatores comuns: observe quais fatores primos aparecem na decomposição de todos os números.
3. Multiplique: o MDC será o produto dos fatores primos comuns, cada um elevado ao seu menor expoente.

Exemplo: Vamos calcular o MDC de 36 e 90.

• Decomposição de 36: 2² x 3²
• Decomposição de 90: 2 x 3² x 5

Os fatores primos comuns são 2 e 3. O menor expoente do 2 é 1 (em 2¹) e o menor expoente do 3 é 2 (em 3²).

MDC(36, 90) = 2¹ x 3² = 2 x 9 = 18.

Método da comparação

Este método é mais intuitivo e funciona bem para números menores. A ideia é listar todos os divisores de cada número e encontrar o maior que eles têm em comum.

1. Liste os divisores: escreva a lista de todos os divisores de cada número.
2. Compare as listas: encontre os números que aparecem em todas as listas (os divisores comuns).
3. Identifique o maior: o maior número entre os divisores comuns é o MDC.

Exemplo: Vamos calcular o MDC de 20 e 30.

• Divisores de 20: {1, 2, 4, 5, 10, 20}
• Divisores de 30: {1, 2, 3, 5, 6, 10, 15, 30}

Os divisores comuns são {1, 2, 5, 10}. O maior deles é 10. Portanto, MDC(20, 30) = 10.

Decomposição simultânea

Este método prático se parece com o cálculo do MMC, mas com uma regra importante: você só pode dividir os números por um fator primo que divida todos eles ao mesmo tempo.

1. Coloque os números lado a lado: escreva os números separados por uma vírgula e trace uma linha vertical à direita.
2. Divida pelos fatores primos comuns: encontre um número primo que divida todos os números simultaneamente e realize a divisão. Anote o primo à direita da linha.
3. Repita o processo: continue dividindo os resultados pelo mesmo ou por outros primos, sempre garantindo que o primo escolhido divida todos os números da linha.
4. Multiplique os fatores: quando não houver mais nenhum primo que divida todos os números ao mesmo tempo, pare. O MDC é o produto dos fatores primos que você anotou.

Exemplo: Vamos calcular o MDC de 48, 60 e 72.

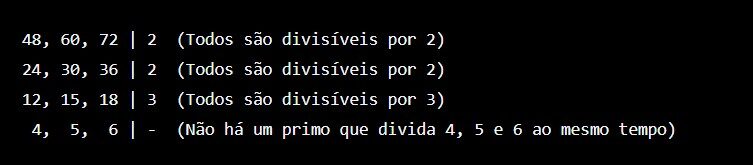
O processo para aqui. Agora, multiplicamos os fatores à direita: 2 x 2 x 3 = 12. Portanto, MDC(48, 60, 72) = 12.

Propriedades do MDC

O Máximo Divisor Comum possui algumas propriedades que podem facilitar cálculos e a compreensão de conceitos mais complexos.

Propriedade 1: Linearidade

Uma propriedade fundamental do MDC é que, se d = mdc(a, b), então o d pode ser escrito como uma combinação linear de a e b. Isso significa que existem números inteiros x e y tais que d = ax + by.

Outra propriedade mais simples e muito útil é: mdc(k*a, k*b) = k * mdc(a, b). Ou seja, o MDC de múltiplos de dois números é o múltiplo do MDC desses números. Por exemplo, mdc(20, 30) = 10. Se multiplicarmos tudo por 2, teremos mdc(40, 60) = 2 * mdc(20, 30) = 2 * 10 = 20.

Propriedade 2: Relação com o MMC

Existe uma relação muito importante entre o MDC e o MMC (Mínimo Múltiplo Comum). Basicamente, para quaisquer dois números inteiros positivos a e b, a seguinte fórmula é válida:

MDC(a, b) * MMC(a, b) = a * b

Essa propriedade é uma mão na roda para resolver questões que envolvem ambos os conceitos. Se você já calculou o MDC, pode encontrar o MMC rapidamente, e vice-versa.

Questões de MMC – Enem e vestibulares

A melhor forma de fixar o conhecimento é praticando. Vamos resolver alguns exercícios de MDC com diferentes níveis de dificuldade.

Exercício 1

Calcule o MDC entre 50 e 75.

• Solução (usando decomposição simultânea):

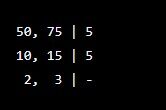
O processo para, pois não há um primo que divida 2 e 3. MDC(50, 75) = 5 x 5 = 25.

Exercício 2

Uma florista tem 40 rosas vermelhas e 64 rosas brancas. Ela quer montar buquês idênticos usando todas as flores, de modo que cada buquê tenha o maior número de rosas possível. Quantos buquês ela poderá montar e qual será a composição de cada um?

• Solução: O problema pede para dividir as flores em grupos iguais do maior tamanho possível. Isso é um caso clássico de MDC. Vamos calcular o MDC(40, 64).

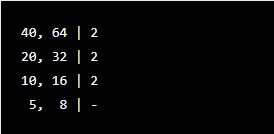
MDC(40, 64) = 2 x 2 x 2 = 8. Isso significa que o maior número de buquês idênticos que ela pode montar é 8.

Para saber a composição de cada buquê:

• Rosas vermelhas: 40 / 8 = 5
• Rosas brancas: 64 / 8 = 7

Resposta: Ela poderá montar 8 buquês, cada um com 5 rosas vermelhas e 8 rosas brancas.

Exercício 3

O produto entre dois números é 1500. Sabendo que o MDC entre eles é 10, qual é o MMC desses dois números?

Solução:

• Este exercício exige o uso da propriedade que relaciona MDC e MMC.
• A fórmula é: MDC(a, b) * MMC(a, b) = a * b.
• Sabemos que a * b = 1500 e MDC(a, b) = 10.
• Substituindo na fórmula: 10 * MMC(a, b) = 1500MMC(a, b) = 1500 / 10MMC(a, b) = 150
• Resposta: O MMC entre esses dois números é 150.

Diferença entre MDC e MMC

É comum confundir MDC e MMC. Embora ambos envolvam divisores e múltiplos, seus objetivos são opostos. Entenda as diferenças:

• MDC (Máximo Divisor Comum): busca o maior número que divide um conjunto de números. A ideia é de divisão e agrupamento.
• MMC (Mínimo Múltiplo Comum): busca o menor número que é múltiplo de um conjunto de números. A ideia é de encontro e coincidência no tempo.

Exemplo prático:

• Problema de MDC: “Quero cortar três tábuas de 12m, 18m e 24m em pedaços iguais do maior tamanho possível”. Você usaria o MDC para encontrar o tamanho máximo de cada pedaço.
• Problema de MMC: “Três ônibus saem de um terminal às 6h. Um sai a cada 12 minutos, outro a cada 18 e o terceiro a cada 24. Quando eles sairão juntos novamente?”. Você usaria o MMC para encontrar o próximo momento de coincidência.

Aplicações do MDC

O cálculo do MDC não é apenas um exercício de matemática. Ele tem aplicações práticas que facilitam nossa vida:

• Simplificação de frações: para simplificar uma fração, você divide o numerador e o denominador pelo MDC entre eles. Por exemplo, para simplificar 18/24, calculamos o MDC(18, 24) = 6. Dividindo ambos por 6, obtemos 3/4.
• Resolução de problemas: o MDC é usado para resolver problemas de divisão em partes iguais e máximas.
• Organização de eventos: para dividir participantes em equipes iguais ou organizar itens em caixas, o MDC ajuda a encontrar a melhor distribuição.
• Construção: para ladrilhar uma área retangular com o menor número de ladrilhos quadrados (ou seja, com o maior ladrilho possível), você calcula o MDC das dimensões da área.

Conclusão

Aprender o que é o Máximo Divisor Comum e como calcular é um passo importante para fortalecer sua base em matemática. Ele não é apenas um conceito teórico, mas uma ferramenta prática para resolver problemas do dia a dia e questões de vestibulares e concursos.