Aprender o cálculo do MMC (Mínimo Múltiplo Comum) é um passo fundamental na matemática básica, abrindo portas para a resolução de diversos problemas aritméticos, desde o ensino fundamental até o vestibular. Hoje, vamos explicar o que é o Mínimo Múltiplo Comum, explorar diferentes métodos de calculá-lo, entender suas propriedades e ver como ele se aplica na prática com exercícios resolvidos. Vamos começar?
Conteúdo
O que é MMC?
O Mínimo Múltiplo Comum, mais conhecido pela sigla MMC, é o menor número inteiro positivo que é múltiplo de dois ou mais números inteiros ao mesmo tempo. Confuso? Vamos simplificar.
Imagine que você tem os números 4 e 6. Os múltiplos de 4 são: 4, 8, 12, 16, 20, 24, … Os múltiplos de 6 são: 6, 12, 18, 24, 30, …
Se você observar as duas listas, verá que existem vários múltiplos em comum, como o 12 e o 24. O MMC é o menor desses múltiplos comuns. Nesse caso, o MMC de 4 e 6 é 12.
O MMC é uma ferramenta essencial na aritmética, principalmente para somar e subtrair frações com denominadores diferentes, um tópico que veremos mais adiante. Por isso, entender o MMC facilita a resolução de problemas e torna a matemática muito mais lógica.
Como calcular o MMC?
Existem diferentes caminhos para encontrar o Mínimo Múltiplo Comum. Embora todos levem ao mesmo resultado, alguns métodos podem ser mais práticos dependendo dos números envolvidos. Conheça os três principais métodos para calcular o MMC.
Método 1: comparação dos múltiplos
Este é o método mais intuitivo e o que usamos no nosso primeiro exemplo. Ele consiste em listar os múltiplos de cada número até encontrar o primeiro que aparece em todas as listas.
Exemplo: Calcular o MMC de 8 e 12.
- Listar os múltiplos de 8: 8, 16, 24, 32, 40, 48, …
- Listar os múltiplos de 12: 12, 24, 36, 48, 60, …
O primeiro número que aparece em ambas as listas é o 24. Portanto, o MMC(8, 12) = 24.
Embora seja simples para números pequenos, este método pode se tornar trabalhoso com números maiores.
Método 2: decomposição em fatores primos
Este método, também conhecido como fatoração, é mais eficiente para números maiores. Ele se baseia na ideia de que todo número inteiro pode ser escrito como um produto de fatores primos.
Exemplo: Calcular o MMC de 12 e 18.
- Fatore cada número em seus fatores primos:
- 12 = 2 x 2 x 3 = 2² x 3¹
- 18 = 2 x 3 x 3 = 2¹ x 3²
- Selecione todos os fatores primos (comuns e não comuns) com seus maiores expoentes:
- Os fatores primos envolvidos são 2 e 3.
- O maior expoente do 2 é ² (do número 12).
- O maior expoente do 3 é ² (do número 18).
- Multiplique esses fatores:
- MMC(12, 18) = 2² x 3² = 4 x 9 = 36
O MMC de 12 e 18 é 36.
Método 3: divisões sucessivas
Este é o método mais popular e prático para calcular o MMC de dois ou mais números simultaneamente. Ele combina a decomposição em fatores primos de forma mais direta.
Exemplo: Calcular o MMC de 15, 20 e 30.
- Coloque os números lado a lado, separados por vírgulas, e trace uma linha vertical à direita.
15, 20, 30 | - Comece a dividir os números pelo menor número primo possível (2, 3, 5, etc.). Se um número não for divisível, repita-o na linha de baixo.

3. Quando todos os números chegarem a 1, o processo termina. O MMC é o produto dos números primos que você usou como divisores.
MMC(15, 20, 30) = 2 x 2 x 3 x 5 = 60
Propriedades do MMC
O Mínimo Múltiplo Comum possui algumas propriedades que podem simplificar os cálculos e a compreensão:
- Relação com o MDC: o produto entre o MMC e o MDC (Máximo Divisor Comum) de dois números é igual ao produto dos próprios números.
- Fórmula: MMC(a, b) x MDC(a, b) = a x b
- Exemplo: MMC(8, 12) = 24 e MDC(8, 12) = 4. Então, 24 x 4 = 96, e 8 x 12 = 96.
- Múltiplos entre si: se um número é múltiplo de outro, o MMC entre eles será o maior dos dois números.
- Exemplo: MMC(6, 18) = 18, pois 18 é múltiplo de 6.
- Números Primos entre Si: se dois números são primos entre si (ou seja, o único divisor comum é 1), o MMC deles é simplesmente o produto entre eles.
- Exemplo: MMC(7, 10) = 7 x 10 = 70.
- MMC com o número 1: o MMC entre qualquer número e 1 será sempre o próprio número.
- Exemplo: MMC(25, 1) = 25.
MMC e Frações
Uma das aplicações mais importantes do MMC é na adição e subtração de frações com denominadores diferentes. Para realizar essas operações, é necessário que as frações tenham um denominador comum, e o MMC é a escolha ideal para encontrar o menor denominador possível, simplificando os cálculos.
Exemplo: Calcular 1/6 + 3/8.
- Encontre o MMC dos denominadores (6 e 8).
- Usando o método das divisões sucessivas:
6, 8 | 23, 4 | 23, 2 | 23, 1 | 31, 1 | - MMC(6, 8) = 2 x 2 x 2 x 3 = 24.
- Usando o método das divisões sucessivas:
- Reescreva as frações com o novo denominador (24). Para isso, divida o novo denominador (24) pelo denominador antigo e multiplique o resultado pelo numerador.
- Para 1/6: 24 ÷ 6 = 4. Então, 4 x 1 = 4. A nova fração é 4/24.
- Para 3/8: 24 ÷ 8 = 3. Então, 3 x 3 = 9. A nova fração é 9/24.
- Agora, some as frações com o mesmo denominador:
- 4/24 + 9/24 = 13/24.
Diferença entre MMC e MDC (Máximo Divisor Comum)
É comum confundir MMC com MDC, mas eles representam conceitos opostos. Veja a diferença de cada um deles:
- MMC (Mínimo MÚLTIPLO Comum): refere-se ao menor número que pode ser dividido pelos números dados. O resultado é sempre maior ou igual ao maior dos números. Geralmente, o MMC é usado para encontrar um ponto comum no futuro, como em problemas de frequência ou ciclos.
- MDC (Máximo DIVISOR Comum): trata-se do maior número que pode dividir os números dados. O resultado é sempre menor ou igual ao menor dos números. É usado para dividir ou agrupar coisas em partes iguais da maior forma possível.
Exemplo comparativo: MMC e MDC de 12 e 18.
- MMC(12, 18) = 36. (36 é o menor número que pode ser dividido tanto por 12 quanto por 18).
- MDC(12, 18) = 6. (6 é o maior número que divide tanto o 12 quanto o 18).
Exercícios de MMC no Enem e vestibulares
Questão 180 – ENEM 2ª Aplicação – 2° Dia 2016
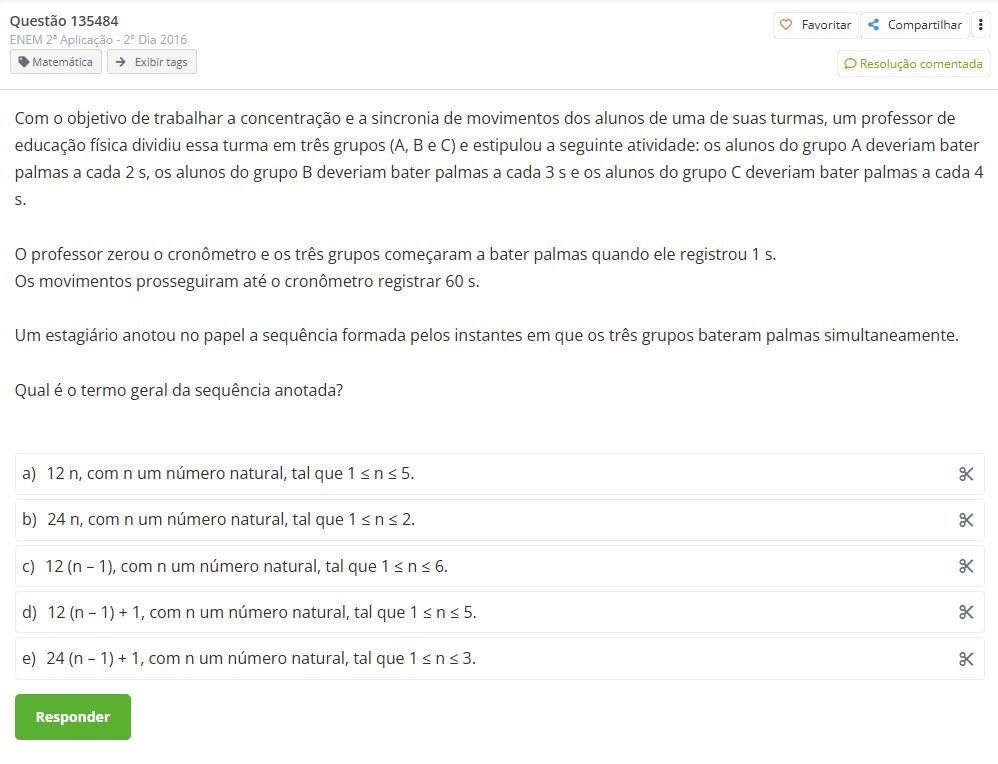
Resolução:
Utilizaremos a progressão aritmética.
Calculando o MMC de 2,3,4, temos que é igual a 12. Sabendo que as palmas iniciaram em 1 segundo com o intervalo de repetição de 12 segundos, forma-se uma P.A.: (1,13,25,37,49). Logo, apenas com n entre 1 e 5, pois n=6 passaria de 60 segundos. A lei de formação da P.A.? an= 1+(n-1).12.
Alternativa D está correta.
Questão 162 – ENEM 2° Dia (Amarela) 2015
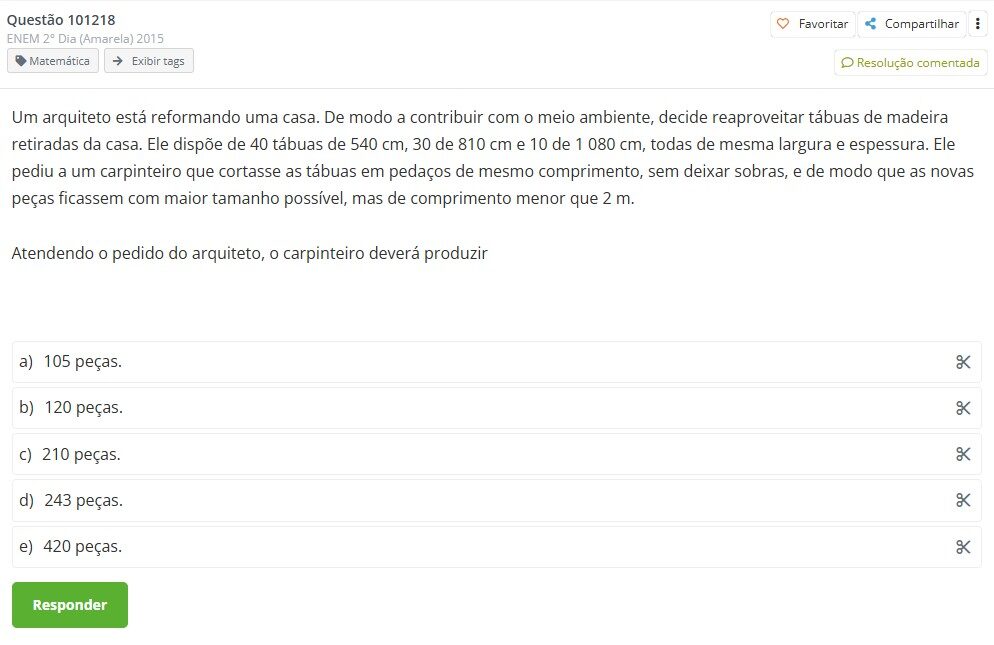
Resolução:
Descobrindo o mdc entre 400 e 320, temos que o valor é 80. Desse modo, estarão disponíveis para cada escola 80 ingressos, sendo 720 ingressos ao todo, temos que o número de escolas escolhidas é:

Dicas e truques para calcular o MMC
Para fechar, confira algumas dicas de matemática que podem melhorar seus cálculos:
- Verifique se um número é múltiplo do outro: antes de começar qualquer cálculo, veja se o maior número é divisível pelos outros. Se for, ele é o MMC.
- Identifique números primos entre si: se os números não têm fatores primos em comum (além de 1), o MMC é simplesmente a multiplicação entre eles. Ex: MMC(9, 10) = 90.
- Organize-se: ao usar o método das divisões sucessivas, mantenha os números alinhados em uma tabela para evitar erros.
- Busque recursos visuais: se você aprende melhor vendo, assista por videoaulas sobre MMC. Muitos tutoriais de matemática online explicam o processo passo a passo de forma visual e didática.
Com essas explicações e dicas, o cálculo do MMC se tornará uma tarefa muito mais simples e intuitiva, ajudando você a avançar com confiança nos seus estudos de matemática.








