A regra de três é um dos conceitos matemáticos mais utilizados no dia a dia. Seja para calcular descontos, converter medidas ou resolver problemas no Enem e vestibulares, esse método facilita a determinação de um valor desconhecido a partir de uma relação entre outras grandezas conhecidas.
Hoje vamos explicar de forma clara e objetiva, como utilizar a regra de três simples e composta, com exemplos práticos para facilitar o entendimento. Confira! 👇
Conteúdo
O que é a regra de três?
A regra de três é um método matemático utilizado para encontrar um valor desconhecido com base em pelo menos três outros valores conhecidos que mantêm uma relação proporcional. Ela pode ser aplicada em situações do dia a dia, como conversão de unidades, cálculo de porcentagens e estimativas de tempo e produção.
Como usar regra de três?
Para resolver uma regra de três em um exercício, siga estes passos:
- Identifique as grandezas envolvidas: verifique se os valores conhecidos estão relacionados diretamente ou inversamente;
- Monte uma proporção: organize os valores em uma tabela, alinhando as grandezas semelhantes;
- Multiplique em cruz: multiplique os valores de forma cruzada para encontrar a equação;
- Resolva a equação: divida o produto dos valores e encontre o valor desconhecido.
Exemplo prático de regra de três ✍
Para entender na prática, veja:
✍ Problema:
Se 5 maçãs custam R$10, quanto custarão 8 maçãs?
✍ Solução:
1. Identifique as grandezas:
- Número de maçãs
- Custo
2. Organize os dados em uma tabela:
| Maçãs | Custo (R$) |
| 5 | 10 |
| 8 | x |
3. Verifique a proporcionalidade:
- Se o número de maçãs aumenta, o custo também aumenta.
- Portanto, a relação é diretamente proporcional.
4. Monte a proporção:
5/8 = 10/x
5. Resolva a equação:
5x = 8 * 10
5x = 80
x = 80 / 5
x = 16
✍ Resposta: 8 maçãs custarão R$16.
👉 Lista de Exercícios: teste seus conhecimentos para o Enem!
Tipos de regra de três: simples e composta
A regra de três pode ser classificada em dois tipos principais: simples e composta. A escolha do tipo depende do número de grandezas envolvidas na relação.
Regra de três simples
A regra de três simples é utilizada quando há apenas duas grandezas diretamente ou inversamente proporcionais.
✍ Diretamente proporcional: quando uma grandeza aumenta, a outra também aumenta.
Exemplo: Se 2 litros de tinta cobrem 8m², quantos litros serão necessários para cobrir 24m²?
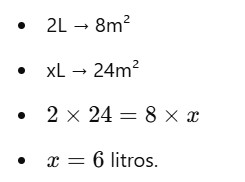
✍ Inversamente proporcional: quando uma grandeza aumenta, a outra diminui.
Exemplo: Se 4 trabalhadores terminam um serviço em 12 dias, em quantos dias 6 trabalhadores fariam o mesmo trabalho?
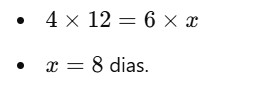
Regra de três composta
A regra de três composta é usada quando há mais de duas grandezas envolvidas. O processo é similar ao da regra de três simples, mas requer análise da relação entre todas as variáveis.
✍ Exemplo: Se 5 máquinas produzem 200 peças em 8 horas, quantas máquinas são necessárias para produzir 300 peças em 6 horas?
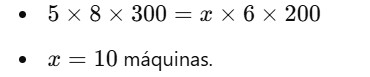
Compreender a regra de três é essencial para resolver questões matemáticas com facilidade. Com prática, você se tornará cada vez mais rápido e eficiente nesses cálculos!
Resumo sobre a regra de três
A regra de três é um método matemático utilizado para resolver problemas envolvendo proporções entre grandezas. Ela permite encontrar um valor desconhecido a partir da relação entre outros valores conhecidos.
Existem dois tipos principais de regra de três:
- Regra de três simples: usada quando há apenas duas grandezas diretamente ou inversamente proporcionais;
- Regra de três composta: aplicada quando há mais de duas grandezas envolvidas, exigindo a análise da relação entre todas elas.
👉 Veja o resumo em esquema de mapa mental:
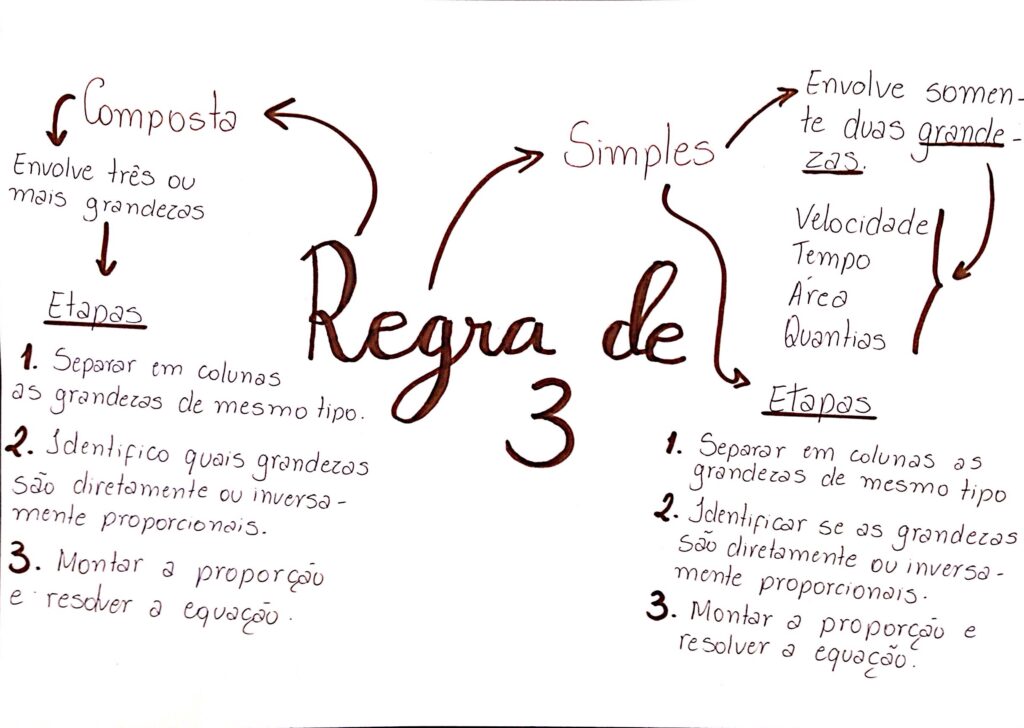
Como a regra de três aparece no Enem e vestibulares?
A regra de três é um dos conceitos matemáticos mais cobrados no Enem e em vestibulares, pois está presente em diversas áreas, como Matemática, Física, Química e até Biologia.
Questões que envolvem proporção, escalas, porcentagens e variações diretas e inversas geralmente exigem o uso desse método.
No Enem, a regra de três aparece em problemas contextualizados, como:
- Cálculo de consumo: determinar a quantidade de combustível necessária para um trajeto, baseado no consumo do veículo;
- Conversão de unidades: transformar medidas, como km para metros ou horas para minutos;
- Análise de tabelas e gráficos: interpretar dados estatísticos e fazer projeções com base na proporcionalidade;
- Cálculo de tempo e trabalho: questões envolvendo produtividade, como o tempo necessário para concluir uma tarefa com diferentes quantidades de trabalhadores.
Dominar a regra de três é essencial para otimizar o tempo de prova, já que ela permite resolver rapidamente problemas que poderiam exigir cálculos mais complexos. Além disso, compreender bem sua aplicação ajuda a evitar erros em questões interdisciplinares.








